|
|
|
A natural equation is an equation which specifies a curve independent of any choice of coordinates or parameterization. The study of natural equations began with the following problem: given two functions of one parameter, find the Space Curve for which the functions are the Curvature and Torsion.
Euler ![]() gave an integral solution for plane curves (which always have Torsion
gave an integral solution for plane curves (which always have Torsion ![]() ). Call the Angle between the Tangent line to the curve and the
x-Axis
). Call the Angle between the Tangent line to the curve and the
x-Axis ![]() the Tangential Angle, then
the Tangential Angle, then
| (1) |
| (2) | |||
| (3) |
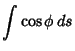 |
(4) | ||
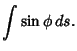 |
(5) |
Among the special planar cases which can be solved in terms of elementary functions are the Circle, Logarithmic Spiral, Circle Involute, and Epicycloid. Enneper showed that each of these is the projection of a Helix on a Conic surface of revolution along the axis of symmetry. The above cases correspond to the Cylinder, Cone, Paraboloid, and Sphere.
See also Cesàro Equation, Intrinsic Equation, Whewell Equation
References
Cesàro, E. Lezioni di Geometria Intrinseca. Napoli, Italy, 1896.
Euler, L. Comment. Acad. Petropolit. 8, 66-85, 1736.
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 111-112, 1993.
Melzak, Z. A. Companion to Concrete Mathematics, Vol. 2. New York: Wiley, 1976.
Struik, D. J. Lectures on Classical Differential Geometry. New York: Dover, pp. 26-28, 1988.
|
|
|
© 1996-9 Eric W. Weisstein