|
|
|
Given a curve ![]() , the pedal curve of
, the pedal curve of ![]() with respect to a fixed point
with respect to a fixed point ![]() (the Pedal Point) is the locus of the
point
(the Pedal Point) is the locus of the
point ![]() of intersection of the Perpendicular from
of intersection of the Perpendicular from ![]() to a Tangent to
to a Tangent to ![]() . The parametric equations
for a curve
. The parametric equations
for a curve ![]() relative to the Pedal Point
relative to the Pedal Point ![]() are
are
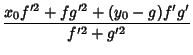 |
|||
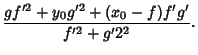 |
| Curve | Pedal Point | Pedal Curve |
| Astroid | center | Quadrifolium |
| Cardioid | cusp | Cayley's Sextic |
| Central Conic | Focus | Circle |
| Circle | any point | Limaçon |
| Circle | on Circumference | Cardioid |
| Circle Involute | center of Circle | Archimedean Spiral |
| Cissoid of Diocles | Focus | Cardioid |
| Deltoid | center | Trifolium |
| Deltoid | cusp | simple Folium |
| Deltoid | on curve | unsymmetric double folium |
| Deltoid | Vertex | double folium |
| Epicycloid | center | Rose |
| Hypocycloid | center | Rose |
| Line | any point | point |
| Logarithmic Spiral | pole | Logarithmic Spiral |
| Parabola | Focus | Line |
| Parabola | foot of Directrix | Right Strophoid |
| Parabola | on Directrix | Strophoid |
| Parabola | reflection of Focus by Directrix | Maclaurin Trisectrix |
| Parabola | Vertex | Cissoid of Diocles |
| Sinusoidal Spiral | pole | Sinusoidal Spiral |
| Tschirnhausen Cubic | Focus of Pedal | Parabola |
See also Negative Pedal Curve
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 46-49 and 204, 1972.
Lee, X. ``Pedal.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Pedal_dir/pedal.html.
Lockwood, E. H. ``Pedal Curves.'' Ch. 18 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 152-155, 1967.
Yates, R. C. ``Pedal Curves.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 160-165, 1952.
|
|
|
© 1996-9 Eric W. Weisstein