|
|
|
A curve which is related to the solution of Lemoine's Problem and its generalization to Isosceles
Triangles constructed on the sides of a given Triangle. The Vertices of the constructed Triangles are
| (1) | |||
| (2) | |||
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
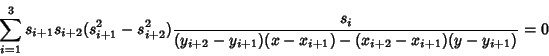 |
(8) |
 |
(9) |
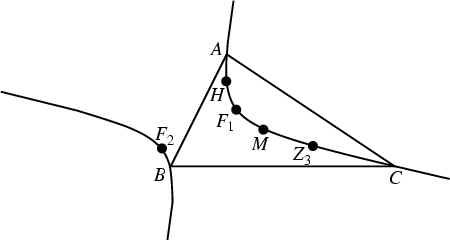
Kiepert's hyperbola passes through the triangle's Centroid ![]() (
(![]() ), Orthocenter
), Orthocenter
![]() (
(![]() ), Vertices
), Vertices ![]() (
(![]() if
if
![]() and
and
![]() if
if
![]() ),
), ![]() (
(![]() ),
), ![]() (
(![]() ), Fermat Point
), Fermat Point ![]() (
(![]() ), second Isogonic
Center
), second Isogonic
Center ![]() (
(![]() ), Isogonal Conjugate of the Brocard Midpoint (
), Isogonal Conjugate of the Brocard Midpoint (![]() ), and
Brocard's Third Point
), and
Brocard's Third Point ![]() (
(![]() ), where
), where ![]() is the Brocard Angle (Eddy and
Fritsch 1994, p. 193).
is the Brocard Angle (Eddy and
Fritsch 1994, p. 193).
The Asymptotes of Kiepert's hyperbola are the Simson Lines of the intersections of the Brocard Axis with the Circumcircle. Kiepert's hyperbola is a Rectangular Hyperbola. In fact, all nondegenerate conics through the Vertices and Orthocenter of a Triangle are Rectangular Hyperbolas the centers of which lie halfway between the Isogonic Centers and on the Nine-Point Circle. The Locus of centers of these Hyperbolas is the Nine-Point Circle.
The Isogonal Conjugate curve of Kiepert's hyperbola is the Brocard Axis. The center of the Incircle of the Triangle constructed from the Midpoints of the sides of a given Triangle lies on Kiepert's hyperbola of the original Triangle.
See also Brocard Angle, Brocard Axis, Brocard Points, Centroid (Triangle), Circumcircle, Isogonal Conjugate, Isogonic Centers, Isosceles Triangle, Lemoine's Problem, Nine-Point Circle, Orthocenter, Simson Line
References
Casey, J. A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing
an Account of Its Most Recent Extensions with Numerous Examples, 2nd rev. enl. ed. Dublin: Hodges, Figgis, & Co., 1893.
Eddy, R. H. and Fritsch, R. ``The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle.''
Math. Mag. 67, 188-205, 1994.
Kelly, P. J. and Merriell, D. ``Concentric Polygons.'' Amer. Math. Monthly 71, 37-41, 1964.
Mineuer, A. ``Sur les asymptotes de l'hyperbole de Kiepert.'' Mathesis 49, 30-33, 1935.
Rigby, J. F. ``A Concentrated Dose of Old-Fashioned Geometry.'' Math. Gaz. 57, 296-298, 1953.
Vandeghen, A. ``Some Remarks on the Isogonal and Cevian Transforms. Alignments of Remarkable Points of a Triangle.''
Amer. Math. Monthly 72, 1091-1094, 1965.
|
|
|
© 1996-9 Eric W. Weisstein